Table of Contents
Application de la cinématique inverse au robot Poppy Torso dans un jeu de morpion
- Présentation du projet
Dans le cadre de notre stage à l'IMT-Atlantique, il nous a été soumis le thème : « Application de la cinématique inverse au robot Poppy Torso dans un jeu de morpion ». L'objectif de ce projet est d'utiliser la cinématique inverse pour simuler le mouvement du robot Poppy Torso dans un jeu de morpion à l'aide du simulateur V-REP. Pour cela nous devons nous appuyer sur les résultats du projet « Main préhensile pour le robot Poppy et interface Tangible » réalisé par un groupe d’élèves ingénieurs de l’IMT-Atlantique pour proposer un autre programme de jeu utilisant la cinématique inverse.
- Description du jeu
Le jeu de morpion est un jeu de réflexion se pratiquant à deux (02) joueurs au tour par tour et dont le but est de créer le premier un alignement sur une grille carrée de 3×3 cases. Chaque joueur dispose à cet effet de cinq (05) pions avec des symboles identiques pour chaque joueur et le gagnant d’une partie du jeu est celui qui arrivera à aligner trois (03) de ses pions horizontalement, verticalement ou en diagonale
Installation de logiciels
Pour la réalisation de notre projet il était nécessaire d'installer certains logiciels.
Toute la documentation pour l'installation de la distribution Anaconda Python, du logiciel poppy et du simulateur V-REP est accessible à travers le lien suivant : https://docs.poppy-project.org/fr/
Installer Python
Le langage Python est le langage que nous avons utilisé pour la programmation de notre robot. Nous avons donc téléchargé puis installé la distribution Python Anaconda. Le lien pour le téléchargement est le suivant : https://www.anaconda.com/download/. Nous avons opté pour la version 2.7.
Installer le logiciel poppy
Pour pouvoir simuler le robot Poppy Torso, l'installation du logiciel Poppy sur Windows dans notre cas a été indispensable. Pour l'installation nous avons exécuté dans l'invité de commande de la distribution Anaconda (Anaconda Prompt) la commande suivante :
pip install poppy-torso
Cette commande permet d'installer tout le nécessaire pour contrôler le robot Poppy Torso. Nous avons par la suite fait une mise à jour du logiciel poppy à travers les commandes suivantes :
pip install pypot --upgrade --no-deps pip install poppy-creature --upgrade --no-deps pip install poppy-torso --upgrade --no-deps
Pour la mise à jour, il est conseillé de mettre à jour pypot (la bibliothèque pour le contrôle des moteurs) et le paquet “creature” séparément.
Installer le logiciel V-REP
Le logiciel V-REP est l'environnement de simulation robotique qui nous permettra de simuler le robot Poppy Torso dans le cadre de notre projet. Il est recommandé d'installer les logiciels Poppy avant d'installer l'outil de simulation robotique V-REP.
Nous avons téléchargé puis installer la version V-REP PRO EDU V3.5.0 rev4. Le lien pour le téléchargement est le suivant : http://www.coppeliarobotics.com/downloads.html.
Pendant l'installation, il faut veiller à installer Visual C++ Redistributable 2010 et Visual C++ Redistributable 2012 . Si les versions de Visual C++ Redistributable 2010 ou Visual C++ Redistributable 2012 sont déjà présentes sur votre ordinateur, il est conseillé de les “réparer”(il s'agit du processus de ré-installation).
Installer le package IKPy
Pour utiliser la cinématique inverse dans notre projet nous avons installé le package IKPy en exécutant dans l'invité de commande de la distribution Anaconda (Anaconda Prompt) la commande ci-dessous :
pip install ikpy
Mouvements de Poppy Torso
Une fois les installation achevées, notre prochaine tâche a été d'identifier les différents mouvements du robot pendant le déroulement du jeu puis de déterminer les coordonnées cartésiennes des points qu'il est censé atteindre pendant une partie de jeu.
Cadrage
L'utilisation de la cinématique inverse dans notre projet permettra au robot Poppy Torso d'atteindre un point M(Xf,Yf,Zf) de notre espace de jeu avec sa main droite en partant d'une position initiale N(Xi,Yi,Zi). En effet, la cinématique inverse calculera automatiquement les différentes positions et rotations des moteurs actifs du bras droit qu'il faut pour atteindre une position désirée.
Compte tenu du fait que la cinématique inverse, dans notre cas, ne s’appliquera qu’aux bras droit du robot Poppy Torso, nous avons focalisé notre travail sur les mouvements effectués par ce bras pendant le déroulement du jeu. Nous avons donc considéré que le robot Poppy Torso se trouve au départ dans sa position juste après le démarrage ou la réinitialisation du jeu.
Nous avons par la suite identifié les différents mouvements du robot pendant le déroulement du jeu puis déterminé les coordonnées cartésiennes des points qu'il est censé atteindre pendant une partie de jeu.
Position initiale des moteurs et de la main droit
Le robot Poppy Torso dispose de treize (13) moteurs qui sont listés dans un ordre bien précis par la commande « poppy.motors ». Nous avons [l_elbw_y ; head_y ; r_arm_z ; head_z ; r_shoulder_x ; r_shoulder_y ; r_elbow_y ; l_arm_z ; abs_z ; bust_y ; bust_x ; l_shoulder_x ; l_shoulder_y].
En nous servant du rapport du projet « Main préhensile pour le robot Poppy et interface Tangible » nous avons pu déterminer la position angulaire de chacun de ses treize (13) moteurs après le démarrage ou l’initialisation du jeu. La position de ces treize (13) moteurs après ajustement est donnée par la liste suivante : « motor_angles_init = [-2,0,-20,-5,-15,10,-10,20,0,0,0,15,-10] ».
Soit le point O (x_main_init, y_main_init, z_main_init) de la position initiale de la main droite du robot dans le repère cartésien. A l’aide de la commande « poppy.r_arm_chain.end_effector » nous avons pu déterminer les coordonnées cartésiennes du point O.
Ainsi nous avons « x_main_init, y_main_init, z_main_init = (-0.19 ; -0.15 ; 0.10) ».
Positions à atteindre pendant une partie de jeu
Pendant le déroulement d’une partie de jeu, le robot Poppy Torso effectue trois (03) principaux mouvements.
Le premier mouvement du robot est de prendre un pion. Pour une partie de jeu le robot peut prendre au total 4 à 5 pions qui sont empilés à une position A (x_pion,y_pion,z_pion_k) bien précise. A ce niveau c’est seulement la hauteur (z_pion_k) de chaque pion qui varie au fur et à mesure que le robot prend un pion.
Une fois qu’un pion est saisi par le robot à l’aide de l’électroaimant, son second mouvement est de placer ce pion dans l’une des cases vides B (xcase,ycase,zcase) de la grille de jeu selon la stratégie de jeu mise en place dans le programme. Le jeu de morpion a neuf (09) cases et le robot doit pouvoir atteindre chacune de ces cases. Le dernier mouvement est le retour à la position. En effet, le robot après la pose d’un pion dans une case du jeu doit revenir à sa position de départ c’est-à-dire la position que nous avons défini comme notre position initiale.
Pour la détermination des coordonnées cartésiennes des neuf (09) cases et des cinq (05) pions nous nous sommes appuyé sur le rapport du projet « Main préhensile pour le robot Poppy et interface Tangible ». Les valeurs utilisées pour la simulation sont résumées dans le tableau ci-dessous.
| Points | Coordonnées cartésiennes (en mètre) | Description |
|---|---|---|
| A | (-0.30,-0.15,0.75) | Position du pion |
| B1 | (-0.10,-0.25,0.75) | Position de la case (0,0) |
| B2 | (0.00,-0.25,0.75) | Position de la case (0,1) |
| B3 | (0.10,-0.25,0.75) | Position de la case (0,2) |
| B4 | (-0.10,-0.20,0.75) | Position de la case (1,0) |
| B5 | (0.00,-0.20,0.75) | Position de la case (1,1) |
| B6 | (0.10,-0.20,0.75) | Position de la case (1,2) |
| B7 | (-0.10,-0.15,0.75) | Position de la case (2,0) |
| B8 | (0.00,-0.15,0.75) | Position de la case (2,1) |
| B9 | (0.10,-0.15,0.75) | Position de la case (2,2) |
Création des objets du projet
Après avoir identifié les mouvements du bras droit de notre robot et déterminé les coordonnées cartésiennes des points à atteindre nous sommes passé à la création des objets du jeu. Toute cette étape s'est faite par programmation en langage Python.
Poppy Torso
La création d'un objet « poppy » exige au préalable l'importation de certains modules. Le code pour l'importation des modules nécessaires et la création de l'objet « poppy » est le suivant :
from pypot.vrep import from_vrep from pypot.creatures import PoppyTorso poppy =PoppyTorso(simulator='vrep')
Grille de jeu et pions
Notre grille de jeu est constituée de 3×3 cases. Comme dimension de chaque case nous avons opté pour une longueur (l'axe des x) de 8 cm, une largeur (l'axe des y) de 4 cm et une hauteur (l'axe des z) de 1 cm. Le robot poppy dispose de 5 pions empilés que nous avons matérialisé par un cylindre de rayon 3 cm et de hauteur de 8 cm. Pour la réalisation de notre espace de jeu nous avons d'abord créé un objet « objet_io » que nous avons instancié à l'interface io du robot afin de pouvoir faire apparaître nos cases et pion sur la table de Poppy Torso du simulateur V-REP. Le code pour l'instanciation de notre objet « objet_io » est le suivant :
objet_io = poppy._controllers[0].io
Nous avons par la suite utilisé les fonctions « objet_io.add_cube() » et « objet_io.add_cylinder() » pour créer respectivement les neuf (09) cases et le pion. La première fonction prend en paramètre le nom , la position, les dimensions et la masse de la case. En plus des paramètres cités pour la première fonction la seconde fonction prend comme dernier paramètre la precision. Le code pour la création du pion et de la case (0,0) est :
name_pion = 'pion' pos_pion = [-0.30,-0.15,0.75] # X, Y, Z sizes_pion = [0.03, 0.03,0.08] # en mètre mass_pion = 2 # en kg precision=[1000,1000] objet.add_cylinder(name_pion, pos_pion, sizes_pion, mass_pion,precision)
name_case = 'case1' # (0.0) pos_case = [-0.10,-0.25,0.75] # X, Y, Z sizes_case = [0.08, 0.04,0.001] # en mètre (x,y,h) mass_case = 2 # en kg objet.add_cube(name_case, pos_case, sizes_case, mass_case)
Application de la cinématique inverse
L'espace de jeu étant créé, nous sommes passé à l'élaboration du programme devant piloter le bras droit du robot Poppy Torso pendant le déroulement du jeu de morpion. A ce niveau nous avons utilisé la fonction « poppy.r_arm_chain.goto() » de la cinématique inverse. Elle prend trois (03) paramètres : les coordonnées cartésiennes de la position à atteindre, le temps pour atteindre la position souhaitée et la mise en attente ou non de l'exécution de la suite du programme. Cette fonction calcule et affecte la position et l'orientation qu'il faut aux sept (07) moteurs [r_elbw_y ; r_arm_z ; r_shoulder_x ; r_shoulder_y ; bust_x ; bust_y ; abs_z] du bras droit de Poppy Torso pour atteindre la position souhaitée. Par défaut seuls les quatre (04) moteurs [r_elbw_y ; r_arm_z ; r_shoulder_x ; r_shoulder_y] sont actifs.
Dans l'application de la cinématique inverse par l'utilisation de la fonction « poppy.r_arm_chain.goto() » nous étions confronté à deux (02) principales difficultés : la première était d'atteindre la position souhaitée c'est-à-dire la position du pion, la position de l'une des cases ou la position initiale sans toucher un obstacle de l'environnement du jeu. La seconde était la forme du mouvement effectué par le bras qui devait être proche de celle d'un humain.
Comme réponse à la première problématique nous avons défini une trajectoire pour les différents positions à atteindre. Afin que le mouvement se rapproche de celui d'un humain nous avons joué sur le pas et le temps d'exécution.
Concernant la trajectoire nous avons défini une trajectoire en cloche pour la prise et la pose d'un pion dans la grille de jeu et une trajectoire rectiligne pour le retour à la position initiale.
Trajectoire en cloche
Nous avons d'abord défini les équations horaires de la trajectoire en supposant que nous avons un mouvement rectiligne uniforme selon l'axe y et un mouvement parabolique dans le plan (O,x,z). La figure illustrant les différentes trajectoires se présente comme suit :
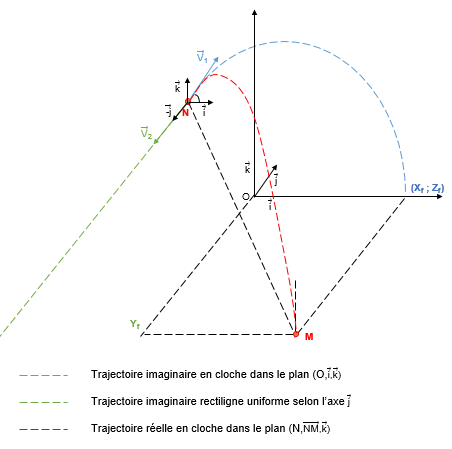 Les équations horaires du mouvement ainsi établies sont :
Les équations horaires du mouvement ainsi établies sont :
X(t)= V1.cos(a).t + Xi Y(t)= V2.t + Yi Z(t)= -1/2.g.t^2 + V1.sin(a).t + Zi
Connaissant les coordonnées cartésiennes de la position initiale N(Xi,Yi,Zi) et de la position finale M(Xf,Yf,Zf) à atteindre par la main droite du robot il était question pour nous de déterminer l'ange « a » que fait la vitesse V1 avec l'axe des abscisses, la vitesse initiale « V1 » de la main droite du robot dans le plan (O,x,z) et la vitesse « V2 » de cette main selon l'axe y tout en s'assurant de ne pas dépasser une certaine hauteur (h = Zmax).
Notre démarche a été la suivante :
- Exprimer V2 en fonction de V1 :
V2 = k.V1.cos(a) avec k = (Yf-Yi)/(Xf-Xi)
- Fixer la valeur de l'ange « a » :
Pour cette valeur de l'angle « a » nous avons chercher à déterminer V1 en utilisant l'expression de la portée qui vaut
Xf = (V1/g).cos(a).[V1.sin(a) + sqrt( (V1.sin(a))^2 + 2.g.(Zi-Zf) )] + Xi.
- Déterminer la valeur de V1 :
A partir de l'expression de Xf précédente nous avons cherché la valeur de V1 (en faisant varier V1) qui donne une valeur de Xf proche de la valeur de Xf à atteindre.
Pour chaque valeur de V1 retenue nous avons vérifié que la hauteur maximale de la main du robot était acceptable en utilisant l'expression
Zmax = (0,5/g).(V1.sin(a))^2 + Zi
Pour terminer nous avons testé les différentes valeurs obtenues dans notre système d'équation horaire du mouvement pour d’éventuel ajustement.
- De la position initiale à la position du pion
A ce niveau nous avons fixé la valeur de l'angle « a » à 2.pi/3 et comme résultats des calculs nous avons obtenu :
V1 = 1,23 m/s Zmax = 14,77 cm
- De la position du pion à la position d'une case
A ce niveau nous avons fixé la valeur de l'angle « a » à pi/4 et comme résultats des calculs nous avons obtenu :
Pour Xf = -0.10 m V1 = 1,26 m/s Zmax = 12 cm
Pour Xf = 0.00 m V1 = 1,60 m/s Zmax = 14,42 cm
Pour Xf = 0.10 m V1 = 1,88 m/s Zmax = 16,88 cm
Trajectoire rectiligne uniforme
Concernant le retour de la main droite du robot de la position d'une case de la grille de jeu à la position initiale nous avons décomposé la trajectoire du mouvement en deux (02) étapes : un mouvement rectiligne uniforme selon l'axe z pour éviter les pions déjà posés et un mouvement rectiligne uniforme dans le plan (O,x,y).
- Mouvement rectiligne uniforme selon l'axe z
Pour le mouvement selon l'axe z, nous avons fait varier la valeur de Z de Zi à Zf en fixant un pas.
Pour Z allant de Zi à Zf avec un pas « pasZ », Zmain = Z
- Mouvement rectiligne uniforme dans le plan (O,x,y)
Pour le mouvement dans le plan (O,x,y) nous avons exprimé Y(t) en fonction de X(t) puis nous avons fait varier la valeur de X de Xi à Xf en fixant un pas « pasX ».
X(t) = Vx.t + Xi Y(t) = Vy.t + Yi
Y(X) = k(X-Xi) + Yi avec k = (Yf - Yi)/(Xf - Xi) Pour X allant de Xi à Xf avec un pas « pasX », Xmain = X et Ymain = k(X-Xi) + Yi
Exécution du programme
L'exécution du programme de jeu se faire en plusieurs étapes.
Exécuter V-REP
Exécutez le logiciel V-REP en faisant un double clic sur l'icône créée sur le bureau lors de l'installation. Une fois l'interface d'accueil de la fenêtre V-REP affichée, vous pouvez fermer les zones « Model browser » et « scene hierarchy » puis réduisez la largeur de la fenêtre de moitié.
Exécuter Jupyter Notebook
Exécutez Jupyter Notebook en faisant également un double clic sur son icône. Vous pouvez faire une recherche dans la liste des applications installées sur votre ordinateur dans le cas où vous ne retrouvez pas l'icône sur votre bureau.
Lorsque vous cliquez sur cette icône, une console « Jupyter Notebook » s'affiche et peu de temps après une page « http://localhost:8888/tree » s’ouvre dans votre navigateur par défaut.
A partir de cette page du navigateur cliquez sur l'onglet « Files » puis accédez au dossier contenant le programme. Une fois dans ce dossier, créez un nouveau « Notebook » en cliquant sur l'onglet « New » puis sur « Python 2 » de la page Jupyter Notebook. Un nouvel onglet intitulé « Untitled » s’ouvre dans votre navigateur.
Copiez et collez dans le champ de saisie de cet onglet le contenu du programme principal nommé « kinematic_torso.py ».
Réduisez la largeur de la fenêtre du navigateur de moitié de sorte à observer également l'interface du simulateur V-REP. Exécutez le programme en cliquant sur la touche « run » de l'onglet Notebook intitulé « Untitled ».
Fonctionnement du programme
Peu de temps après l'exécution du programme le robot Poppy Torso apparaît sur l'interface du simulateur V-REP.
Quelques secondes plus tard le robot adopte sa configuration initiale suivi de la mise en place du pion et des cases de l'espace de jeu.
Au niveau de l'onglet Notebook apparaît un champ invitant l'utilisateur à saisir le nombre de pions à jouer par le robot.
Selon le nombre de pions à jouer par le robot l'utilisateur est invité, pour chaque pion, à indiquer la ligne puis la colonne de la case à atteindre par le robot avec sa main droite. Pour chaque case à atteindre le robot Poppy Torso effectue avec sa main droite :
- une trajectoire en cloche pour se positionner juste au-dessus du pion.
- une trajectoire en cloche pour se positionner juste au-dessus de la case indiquée par l'utilisateur.
- une trajectoire rectiligne pour se retourner à sa position initiale.
La démonstration vidéo est accessible à travers ce lien : https://drive.google.com/open?id=1mVeNc0ZrXjJVIdxTz1_dE-Y4mM9CYqyf